Donation made, but the challenge continues
This weekend, I posted a brainteaser, promising to pay $100 to whomever solved it. Although the decoding algorithm has not yet been discovered, Mr. Batuhan Bozkurt, who found my puzzle through Reddit, did manage to figure out what the second landmark was. He generously suggested that I donate the prize money to Doctors Without Borders. That is an excellent destination for the money, so I was only too happy to oblige:
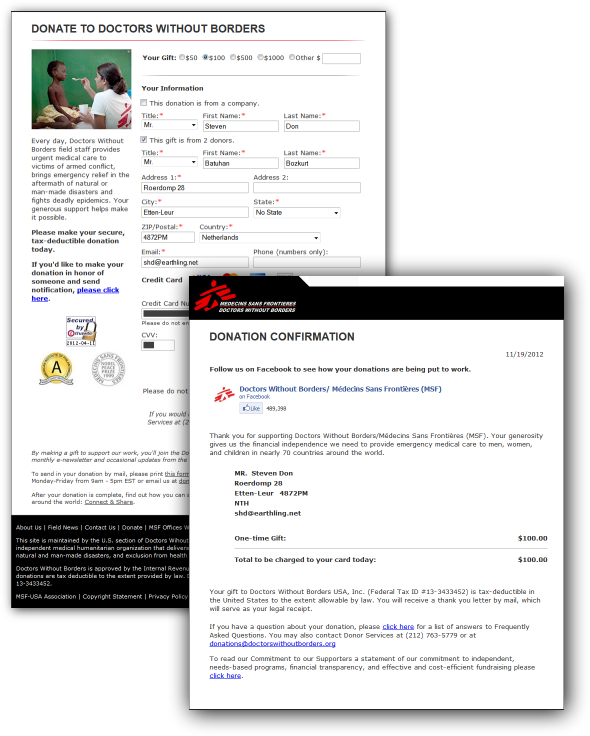
There you go, for discovering the coordinates of the Great Pyramid of Giza and the Eiffel tower, we can do a little to help people in need of medical help in places where such is direly needed.
The challenge continues
As Mr. Bozkurt suggested, the brute force solution is not entirely satisfactory and wouldn't work when there is not a sufficiently large set of input data. Also, it wasn't exactly what I had in mind. I'm still hoping for somebody to discover the actual pattern. I can decode these numbers with pen and paper in a few minutes. Hence the following new and static set of numbers. A second prize of $100 is up for grabs for the person who manages to correctly identify the third landmark and describes how to quickly and easily extract a location encoded in this manner, effectively explaining my manual decoding process.
6549028370
9308377132
5987478672
9318473400
5758758671
1701226107
3203310324
0008077080
7467243472
4977647669
3314933944
1366336361
6388336983
1816904005
6988650225
3313573204
3363677513
1347652260
5327417344
5763780117
5633929510
5633789328
1639733691
5355453454
4762970942
4433939439
5677955559
8611231555
2312372974
9196283474
7640679475
2974972974
4375771374
5333533533
9228589625
5344734475
9690093124
8928733674
0213139200
0884819218
2112313620
9699969279
9327439234
0054403405
1991189118
3502024437
8543814253
1508069550
1872704392
6501959669
9318083111
3576755575
1745858355
8802288202
8244262894
8547446457
0005010510
1551931599
5870416497
0067651597
9732852649
3308156594
5906466417
1366338577
5863902088
3673921092
5301986352
0463999640
4352555243
1871110111
3326333663
5602990599
7074170471
4945744975
9727929597
7635536652
6628076487
2980626975
7411746499
0209674987
3110676987
4227889054
4291147358
8222333112
2326186139
4355737553
7396137966
4542844557
8226082882
2107322072
8676887286
3959753975
8568968982
3193111359
1417213379
0934698929
0098658283
2839081251
1651596922
5980877560
8980546689
8382658012
8917764639
2814515844
8912891188
0387283025
5560755055
7960290920
9117500221
4611511176
8627960562
4129549344
8117918711
9482898892
1057575051
3611444561
4529529555
0326130060
0583633056
8360969080
9120391390
9326988940
9160129317
0526949009
8120357157
0390501233
As before, post a comment with your answer and the process and you might win $100 and a lot of geek cred.
Hints
Try figuring this out on your own as much as possible, without looking in the comments below. If you need a hint, click the button below.
Hint 9: Tbbtyr Zncf yrgf lbh frnepu sbe yngvghqr/ybatvghqr naq frr jung vf ng gung ybpngvba.
Hint 8: Vagrecerg n frdhrapr bs 7 qvtvgf nf 3 qvtvgf sbe qrterrf, 2 qvtvgf sbe zvahgrf, 2 qvtvgf sbe frpbaqf. Gur svefg pbbeqvangr vf (Abegurea) yngvghqr, gur frpbaq pbbeqvangr vf (Rnfgrea) ybatvghqr.
Hint 7: Gubfr cvacbvag na rknpg qvtvg va gur terra oybpx. Gung'f gur bar V'z ybbxvat sbe.
Hint 6: Gurer ner 2 rkprcgvbaf: 1 va n ebj, 1 va n pbyhza.
Hint 5: V pnyy guvf gur "xrl" dhnqenag. Nyy qvtvgf va gur nqwnprag, aba-xrl dhnqenagf nyfb bpphe va gur pbeerfcbaqvat ebjf/pbyhzaf va gur xrl dhnqenag, ohg fbzrguvat vf jebat...
Hint 4: Qenjvat yvarf guebhtu gur oyhr dhnqenagf guebhtu 10 qvtvgf ubevmbagnyyl nf jryy nf iregvpnyyl zrnaf gurl vagrefrpg va gur dhnqenag gung vf bccbfvgr gur terra dhnqenag.
Hint 3: Rnpu oybpx pna guhf or fcyvg hc vagb dhnqenagf bs 5k5 qvtvgf.
Hint 2: Gur 4 qvtvgf va gur zvqqyr bs rnpu oybpx nyjnlf unir 3 bqq qvtvgf (oyhr) naq 1 rira qvtvg (terra).
Hint 1: Gur frg pbafvfgf bs tebhcf bs 10k10 qvtvgf.
Solved!
Redditor Bearasaurus found my puzzle through the Reddit discussion and was the first genius among the clever people in /r/puzzles to have solved the problem. He wins eternal fame and glory, and the $100 prize!
Comments
After some eye-balling the grid, let me make some elimination guesses,
the numbers in the sets shown below cannot be at that set’s position
X: {1}, {8,9}, {6,8}, {4,7}, {5,7}, {6}, {1,4}
Y: {6}, {5,6}, {6}, {7}, {3}, {4,8,9}, {4,6,8}
i.e.,
the solution digit from the first 10x10 matrix is not 1,
the solution digit from the second 10x10 matrix is not 8 or 9, …
You do not have to declare outright the validity of my suspicion, but a nod/shake/wink would help ;)
I think your odds of finding the answer have gotten even better
*** SPOILER ALERT - COMPLETE ANSWER BELOW ***
Step 1: Break puzzle evenly into 2 rows of 7 columns, creating blocks of 10x10 digits each. Each block has a 1-digit solution that is part of the overall coordinates of the solution in the format dddmmss / dddmmss.
Step 2: Solve each 10x10 block separately. First, look at the 4 numbers that form a 2x2 square at the very center of the 10x10 block. Examining only the parity of these 4 numbers, one will be even, three will be odd. The answer is located in the 5x5 quadrant corresponding to the even number. I will use the very first 10x10 block in the new static challenge as an example.
2626513077
6549028370
9308377132
5987478672
9318473400
5758758671
1701226107
3203310324
0008077080
7467243472
At the center is:
47
75
So the answer digit is located in the top left quadrant.
Step 3: To figure out which of the digits in the top left is the answer digit, we compare the lower left quadrant to the lower right quadrant and the upper right quadrant again to the lower right quadrant. Basically, each adjacent quadrant gets compared to the diagonally opposite one. We orient our analysis horizontally if the adjacent quadrant is above or below the answer quadrant and we orient our analysis vertically if the adjacent quadrant is left or right of the answer quadrant. You will do one of each for each 10x10 block. You'll see what I mean when we get started.
Step 3a: Let's start with the lower left - lower right comparison:
57587 58671
17012 26107
32033 10324
00080 77080
74672 43472
We compare horizontally, comparing the 5 digits on the left of each row to the 5 digits on the right of each row. We are looking for a unique digit to exist in our adjacent quadrant (lower left in this case) and NOT in the diagonally opposite one. So comparing:
57587 58671 = left side unique digits are 5,7,8 and all exist at least once on the right
17012 26107 = left side unique digits are 0,1,2,7 and all exist at least once on the right
32033 10324 = left side unique digits are 0,2,3 and all exist at least once on the right
00080 77080 = left side unique digits are 0,8 and all exist at least once on the right
74672 43472 = left side unique digits are 2,4,6,7 and the number 6 DOES NOT EXIST ON THE RIGHT
The 6 is in the 3rd column, meaning the answer digit is in the 3rd column of the answer quadrant.
Step 3b: Now the upper right - lower right comparison:
13077
28370
77132
78672
73400
58671
26107
10324
77080
43472
We compare vertically, comparing the 5 digits on top of each column to the 5 digits on the bottom of each column. We are looking for a unique digit to exist in our adjacent quadrant (upper right in this case) and NOT in the diagonally opposite one. So comparing:
6th column: Upper unique digits are 1,2,7 and all exist at least once below them
7th column: Upper unique digits are 3,7,8 and all exist at least once below them
8th column: Upper unique digits are 0,1,3,4,6 and all exist at least once below them
9th column: Upper unique digits are 0,3,7 and the number 3 DOES NOT EXIST BELOW THEM
10th column: Upper unique digits are 0,2,7 and all exist at least once below them
The 3 is in the 3rd row, meaning the answer digit is in the 3rd row of the answer quadrant.
Step 4: Put it together, the number in the 3rd column and 3rd row of the answer quadrant is: 0
Step 5: Repeat for all other 10x10 blocks.
Here's the column, row, and value of each answer in the subsequent 10x10 blocks:
Block ##: C,R,V
Block 1a: 3,3,0
Block 2a: 8,8,2
Block 3a: 7,2,7
Block 4a: 4,2,1
Block 5a: 4,2,0
Block 6a: 8,3,2
Block 7a: 1,8,9
Block 1b: 7,1,0
Block 2b: 1,8,7
Block 3b: 10,3,8
Block 4b: 2,8,0
Block 5b: 10,4,2
Block 6b: 8,1,3
Block 7b: 8,10,2
The solution is located at: 027°10'29", 078°,02'32" which is the location of the TAJ MAHAL.
Ladies and gentlemen... we have a winner!
Thanks for the prize and thanks for putting together the puzzle! You've made my past few nights quite entertaining, even if the first two nights were full of dead ends =) I look forward to (hopefully) seeing many more of these challenges in the future!
Post a comment